Solving Using Substitution
Substitution
When graphing is not a viable option, systems of equations can be solved symbolically. One method for a symbolic solution is substitution. When solving linear systems using substitution, one variable must be replaced with an equivalent expression that includes the other variable.
Example 1 Solve the following system by substitution.
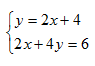
Step 1. Isolate one variable in one equation.
Since y is isolated in the first equation, use that variable and that equation.
Step 2. Substitute the isolated variable's equivalent expression into the other equation.
Since y is equal to 2x + 4, substitute the "y" in 2x + 4y = 6, with the equivalent expression, 2x +4.
2x + 4(2x + 4) = 6
Step 3. Solve the remaining equation.
2x + 8x + 16 = 6
10x +16 = 6
10x = -10
x = -1
Step 4. Substitute the value of the variable found in step 3, into either equation to find the other variable.
y = 2(-1) + 4
y = -2 + 4
y = 2
Therefore the solution point is (-1, 2).