Inverses
| Site: | Clare |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Inverses |
| Printed by: | Guest user |
| Date: | Monday, April 29, 2024, 2:09 AM |
Description
Introduction
Polynomial functions have inverses in special circumstances only. In an earlier unit, inverses of quadratics were discussed. Because the original function did not pass the horizontal line test, quadratics do not have inverses that are functions. Therefore, it makes sense that other even polynomial functions will not have inverses that are functions either. For example, the graph below looks like a parabola and will not have an inverse function.
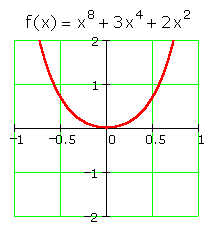
Odd Polynomials
For odd polynomials that have several terms, they will only have an inverse if the sum of these terms is always increasing or always decreasing. Adding together terms that have odd powers with positive coefficients will create a graph that is continuously increasing and will therefore have an inverse that is a function. Another way to determine if the function has an inverse is by graphing the original function and then checking to see if the graph passes the horizontal line test. The horizontal line test asks the question, "Will a horizontal line pass through the graph and touch the graph in only one point?" If the graph passes the horizontal line test, the inverse will be a function.
Example 1
Does the function 
have an inverse function?
Step 1. Does the function have only odd exponents?
Yes, it does.
Step 2. Are the terms of the function always added together?
Yes, they are.
Step 3. Does each term have a positive coefficient?
Yes, they do.
Step 4. Make a graph to check if the function passes the horizontal line test.
Since any horizontal line drawn would intersect the function at exactly one point, then the function's inverse will be a function.
Example 2
Does the function 
have an inverse function?
Step 1. Does the function have only odd exponents?
No, it does not.
Step 2. Are the terms of the function always added together?
Yes, they are.
Step 3. Does each term have a positive coefficient?
Yes, they do.
Step 4. Make a graph to check if the function passes the horizontal line test.
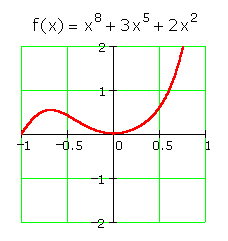
The function does not pass the horizontal line test because a horizontal line would intersect this function at multiple points. The function's inverse will not be a function.
Example 3
Does the function 
have an inverse function?
Step 1. Make a graph to check if the function passes the horizontal line test.
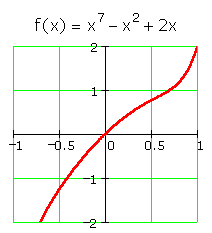
The function passes the horizontal line test. The function's inverse will be a function.
Summary
In later mathematics classes, you will learn a simple method that will quickly tell you if a given polynomial equation represents a function that is always increasing or always decreasing. The topic is beyond the scope of this course. For now, graphing the original function and its possible inverse is a good way to determine if the inverse will be a function.
Finding Inverses
In an earlier discussion about finding inverses, three different methods were discussed. One way is to switch x and y in the equation and solve for y. However, because of the multiple terms and powers of a polynomial, this process can be difficult to do. Graphing the polynomial and using the horizontal line test is a fairly easy method to determine if a polynomial's inverse is a function.
If the graph does not pass the horizontal line test, the polynomial will not have an inverse that is a function so there will not be a need to graph it. If the horizontal line test determines the polynomial function has an inverse function, graph the inverse by following the steps below:
Step 1. Identify several points (x, y) on the graph of the given function.
Step 2. Switch the x- and y-coordinates of each point to form the points (y, x) for the inverse function.
Step 3. Plot the new points and connect them with a smooth curve.
The graph of the inverse should be a reflection of the polynomial's graph across the y = x line.
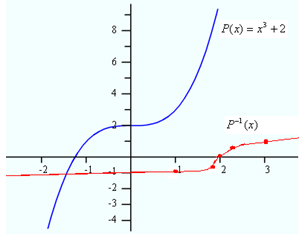
Example 1
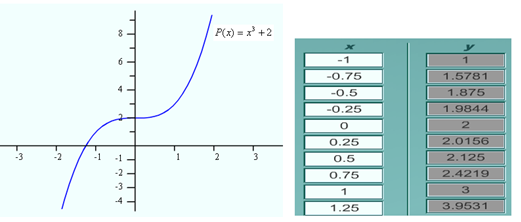
Is there an inverse function for the function 
? If so, graph it.
Step 1. Graph the function.
Step 2. Does it pass the horizontal line test?
Yes it does, so the inverse will be a function.
Step 3. Identify several points (x, y) on the graph of the given function.
Using the table next to the graph above, the points selected will be:
(-1, 1), (-0.5, 1.875), (0, 2), (0.5, 2.125) and (1, 3)
Step 4. Switch the x- and y-coordinates of each point to form the points (y, x) for the inverse function.
(1, -1), (1.875, -0.5), (2, 0), (2.125, 0.5) and (3, 1)
Step 5. Plot the new points and connect them with a smooth curve.
Example 2
Is there an inverse function for the function 
? If so, graph it.
Step 1. Graph the function.
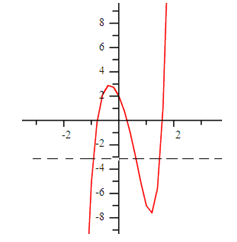
Step 2. Does it pass the horizontal line test?
It does not. Therefore, there will not be an inverse function.
Practice
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing" refresh your browser.
Answer Key
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing" refresh your browser.
Sources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
"Graphing an Inverse Function." http://www.sofsource.com/graphing-an-inverse-function.html (accessed 08/12/2010).
"Inverse Polynomial Functions." http://www.wmueller.com/precalculus/ newfunc/invpoly.html (accessed 08/12/2010).