Transformations
| Sitio: | Clare |
| Curso: | Michigan Algebra I Sept. 2012 |
| Libro: | Transformations |
| Imprimido por: | Cuenta visitante |
| Día: | martes, 16 de diciembre de 2025, 12:43 |
Descripción
Rules
Transformations of one polynomial function were discussed in the quadratic unit. To translate the graph of a quadratic function, we can use the vertex form of a quadratic function, f(x) = a(x - h)2 + k. The transformations followed these rules:
- f (x) + k is f(x) shifted upward k units
- f (x) - k is f(x) shifted downward k units
- f (x + h) is f(x) shifted left h units
- f (x - h) is f(x) shifted right h units
- -f(x) is f(x) flipped upside down ("reflected about the x-axis")
- f (-x) is the mirror of f(x) ("reflected about the y-axis")
- af(x) stretches the graph vertically if a > 1
- af(x) shrinks the graph vertically if 0 < a < 1
Example
If the parent function is f(x) = x2, how does the graph of the function
f(x) = (x - 3)2 + 4 compare?
Step 1. How does the graph move right or left?
The number inside the parentheses is -3, therefore the graph moves right 3.
Step 2. How does the graph move up or down?
The number outside the parentheses is + 4, therefore the graph moves up 4.
Step 3. What does the new graph look like?
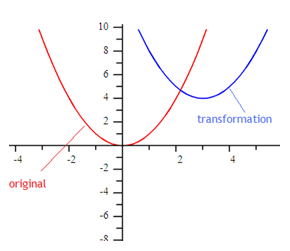
*Note: Other even polynomials will have transformations similar to those of quadratic functions but with some differences.
Cubic Polynomials
Odd polynomials have some similarities to quadratic transformation as well, but with some differences. The simplest case is the cubic function. Cubic functions can be sketched by transformation if they are of the form f (x) = a(x - h)3 + k, where a is not equal to 0. Note that this form of a cubic has an h and k just as the vertex form of a quadratic. However, this does not represent the vertex but does give how the graph is shifted or transformed. The horizontal shift is given by the h. The vertical shift is given by the k.
The simplest cubic function, or parent function, is f(x) = x3, where a = 1 and both h and k = 0, as in f(x)=1(x - 0)3 + 0. How is the parent function transformed if the function becomes f( x) = (x - 2)3 + 3? The parameters a, h, and k are 1, 2, and 3, respectively. These parameters make the graph of the standard function, f(x) = x3, shifted 2 units right and 3 units up, as you can see below:
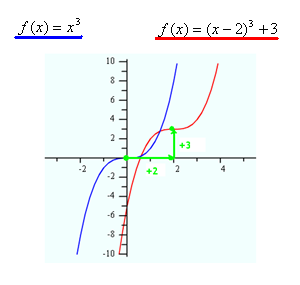
Example 1
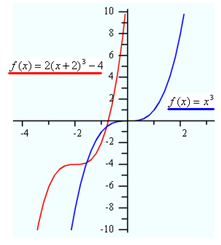
What transformation of ![]() creates the following function?
creates the following function?
![]()
Step 1. How does the a-value affect the graph?
An a-value of 2 will cause a dilation or stretching by a factor of 2 along the y-axis (steeper).
Step 2. How does the h-value affect the graph?
An h-value of 2 will cause a shift of 2 units left.
Step 3. How does the k-value affect the graph?
A k-value of -4 will cause a shift of 4 units down.
Example 2
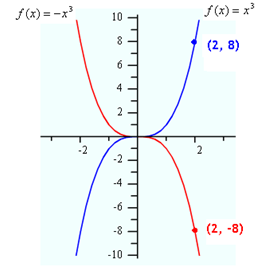
What transformation of ![]() creates the following function?
creates the following function?
![]()
The negative sign is "outside" of the function, so this transformation will be a reflection over the x-axis.
Video Lesson
To learn more about transformations of polynomials, select the following link:
Exploration
Transforming Polynomials Exploration
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Practice
Transforming Cubic Equations Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Transforming Cubic Equations Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser
Sources
Britannica Study Guide, "Creating Graphs by Transformations." http://school.eb.com/lm/studyguides/483/mainframes.html (accessed 08/17/2010).
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Translating a Polynomial Function." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=6458/6458.xml (accessed 9/6/2010).