Print bookPrint book

Standard Form

Site: Clare
Course: Michigan Algebra I Sept. 2012
Book: Standard Form
Printed by: Guest user
Date: Saturday, November 23, 2024, 11:23 PM

Description

Standard Form

Table of contents

Introduction

The standard form of a quadratic equation is ax2 + bx + c = 0 where a, b, and c are real numbers and aunequal 0. Earlier in this unit, vertex form and factored form were discussed. There is a similarity between all three forms. The "a" in the standard form is the same "a" as in the factored and vertex form. That is, the a will always have exactly the same value. To determine the values of a, b, and c, write the equation in standard form.

Example 1 Find the a, b, and c values of the equation: x2 - 3x = 28.

Step 1. Put the equation in standard form.

1x2 - 3x - 28 = 0

Step 2. Identify the a, b, and c values.

a = 1, b = -3, c = -28

Example 2 Find the a, b, and c values of the equation: 5x2 = -45.

Step 1. Put the equation in standard form.

5x2 + 0x + 45 = 0

Step 2. Identify the a, b, and c values.

a = 5, b = 0, c = 45

Exploration Activity

Investigating Standard Form Activity

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Standard Form Exploration Activity Answer Key

 

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Guided Practice

To solidify your understanding of graphing quadratic equations in standard form, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice

Practice

Standard Form Graphing Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Standard From Graphing Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Standard to Vertex Form

Converting from standard to vertex form can be done by finding the x-and y- coordinates of the vertex. The formula for finding the x-coordinate of the vertex is ConvertStand1 . The x-coordinate is used to find y and the "a" values are the same.

Example Rewrite y = 3x2 - 6x + 7 in vertex form.

Step 1. Find the x-coordinate of the vertex.

ConvertStand2

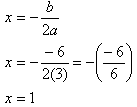
Step 2. Find the y-coordinate of the vertex.

ConvertStand3

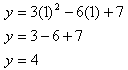
Step 3. Rewrite the equation in vertex form.

Completing the Square

It is also possible to convert standard form to vertex form by completing the square. Completing the square was discussed in an earlier lesson. Now, apply the process to conversion.

Example Convert y = x2 + 4x - 7 to vertex form.

Step 1. If the a-value is not one, divide so that a = 1.

In this equation, a = 1.

Step 2. Move the constant to the other side of the equation.

ConvertSq1

Step 3. Add the constant that will create a perfect square trinomial to each side.

ConvertSq2

Step 4. Factor and simplify.

ConvertSq3


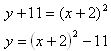
Practice

Converting Standard to Vertex Form Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Converting Standard to Vertex Form Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Coffman, Joseph. "Translating Parabolas." http://www.jcoffman.com/Algebra2/ch5_3.htm (accessed 07/25/2010).

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

Holt, Rinehart & Winston, "Quadratic Functions and Equations ." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch09_03_homeworkhelp.html (accessed 8/22/2010).

Kuta Software, "Free Algebra 2 Worksheets." http://www.kutasoftware.com/freeia2.html (accessed 08/05/2010).