Print bookPrint book

Vertex Form

Site: Clare
Course: Michigan Algebra I Sept. 2012
Book: Vertex Form
Printed by: Guest user
Date: Sunday, November 24, 2024, 12:50 AM

Description

Vertex Form

Table of contents

Introduction

Quadratic Functions can be written in three different forms. The last lesson discussed the standard form of a quadratic. This lesson will discuss vertex form of a quadratic. The vertex form of a quadratic equation is:

y = a(x-h)2 + k

Properties of Graphs in Vertex Form:

  • When a is positive the graph opens upward; when a is negative the graph opens downward
  • When h is positive the graph shifts right; when h is negative the graph shifts left.
  • When k is positive the graph shifts up; when k is negative the graph shifts down.
  • The vertex is the point ( h, k ) and the axis of symmetry is the line x = h .

Naming the Vertex

To find the vertex of an equation in vertex form, locate the h and k of the equation: y = a(x - h) 2 + k. Because the formula subtracts h, the x-coordinate of the vertex will have the opposite sign as the h in the equation. Since the formula adds k, the y-coordinate will have the same sign as the k in the equation.

Example 1 Name the vertex for the function, y = (x - 2)2 + 3.

The vertex is (2, 3).

Example 2 Name the vertex for the function, y = -2(x + 3)2.

The vertex is (-3, 0).

Example 3 Name the vertex for the function, y = -x2 - 4.

The vertex is (0, -4).

Graph a Parabola

When graphing vertex form, first find and graph the vertex (h , k) and axis of symmetry, x = h . Next find the y-intercept by substituting x = 0 into the equation and solving for y . Finally, use the axis of symmetry and y -intercept to plot a symmetry point. Connect the points in a U-shaped curve.


Example

Graph the function: y = (x - 2)2 - 1.

Step 1. Find the vertex and axis of symmetry.

For this equation, the vertex is (2, -1) and the axis of symmetry is x = 2.

Step 2 . Find the y-intercept.

y = (0 - 2)2 - 1

y = (-2)2 -1

y = 4 - 1

y = 3

The y-intercept is (0, 3).

Step 3. Use the y-intercept and axis of symmetry to find another point.

Since (0, 3) is 2 units away from x = 2, the corresponding point is 2 units on the other side of the axis, therefore a point on the graph is (4, 3).

Step 4. Plot the points determined and sketch the curve.

ParabolaGraph

Graphing from a Table

A graph can also be made by making a table of values. Start by finding the vertex as before. Then, because a parabola is symmetric, find a couple of values on either side of the vertex. Plot the points.

Example Graph y = (x - 2)2 - 3 by making a table of ordered pairs.

Step 1. Find the vertex.

For this equation, the vertex is (2, -3).

Step 2. Make a table. Put the vertex in the middle and pick 2 x-values on each side of the vertex.

x

0

1

2

3

4

y



-3




Example Continued

Step 3. Substitute x-values from the table into the equation to fill in the y-values.

y = (0 - 2)2 - 3, y = 1

y = (1 - 2)2 - 3, y = -2

y = (3 - 2)2 -3, y = -2

y = (4 - 2)2 - 3, y = 1

x

0

1

2

3

4

y

1

-2

-3

-2

1

*Note: The table will have symmetrical values on each side of the vertex.

Step 4. Plot the points from the table and sketch the curve.

GraphTable

Practice

To explore more about the vertex form, select the link below:

Exploring Vertex Form #1

To use a calculator to explore vertex form:

Exploring Vertex Form #2

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Keys

Exploring Vertex Form #1 Answer Key

Exploring Vertex Form #2 Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Equation from a Graph

Most applications of quadratic functions will require a model to be written. It is possible to write a model when given a graph, table, or a couple of points.

To write an equation from a graph, first locate the vertex and one other point. Substitute the vertex and point into the vertex form and then solve for the a-value.

Example Write the equation of the parabola shown below:

EquationGraph1-1

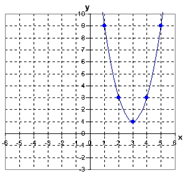
Step 1. Find the vertex and one other point.

The vertex is (3, 1) and another point on the graph is (5, 9).

Step 2. Substitute the vertex and point into the formula and solve for the a-value.

EquationGraph1-2

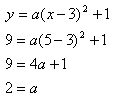
Step 3. Write the equation of the parabola in vertex form.

Given the Vertex and a Point

When given the vertex and a point without the graph, the steps will work the same way.

Example What is the equation of a parabola with a vertex at (1 , - 8) and passes through the point (2 , - 6)?

Step 1. Substitute the vertex and point into the formula and solve for the a-value.

GivenVertex1-1

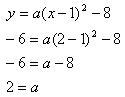
Step 2. Write the equation of the parabola in vertex form.

GivenVertex1-2


Practice

Vertex Form of a Parabola Worksheet

Properties of Parabolas Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Keys

Vertex Form of a Parabola Answer Key

Properties of Parabolas Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Coffman, Joseph. "Translating Parabolas." http://www.jcoffman.com/Algebra2/ch5_3.htm (accessed 07/25/2010).

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

"Vertex and Intercepts Parabola Problems." http://www.analyzemath.com/quadratics/vertex_problems.html (accessed 07/25/2010).