Multiplying & Dividing
| Site: | Clare |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Multiplying & Dividing |
| Printed by: | Guest user |
| Date: | Sunday, November 24, 2024, 12:52 AM |
Description
Multiplying and Dividing
Introduction
Multiplying and dividing functions will require more steps than adding and subtracting functions. While this topic will be covered more thoroughly in the Polynomial Unit, multiplying of linear terms and dividing by a monomial will be discussed here.
The function notation for multiplying and dividing is very similar to adding and subtracting. When multiplying functions, 
When dividing two functions, 
, where 
because division by zero is an undefined operation in mathematics.
Multiplying
When multiplying a monomial (or one term expression) by a binomial (or two-term expression), the Distributive Property will be used to multiply the two functions.
Example Given 
and 
, find 
.
Step 1. Replace f(x) and g(x) with their equivalent expressions.
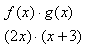
Step 2. Use the Distributive Property to multiply and simplify.
For a review of the Distributive Property, select the following link:
FOIL Method
One method that can be used when multiplying two binomials is the FOIL method. FOIL stands for First, Outer, Inner, and Last. These letters help to remember to multiply each term in the first binomial by each term in the second binomial using the Distributive Property.
Example Given 
and 
, find 
.
Step 1. Replace f(x) and g(x) with their equivalent expressions.
Step 2. Multiply the First, Outer, Inner, and Last terms of each binomial.
First + Outer + Inner + Last
+ 
+ 
+ 
Step 3. Simplify the expressions.
For a review of the FOIL method of multiplying, please select the following link:
Interactive Activity
To solidify your understanding of multiplying two binomials, select the following link:
Practice
Answer Key
Dividing
When dividing two functions, 
, remember that g(x) 
since division by zero is undefined. To divide a polynomial by a monomial, divide each term of the polynomial by the monomial. Remember to watch the signs of the terms when dividing and that a number divided by itself is one, do not cancel these terms.
Example 1
Given f(x) = 5x + 35 and g(x) = 5, find 
.
Step 1. Replace f(x) and g(x) with their equivalent expressions.
Step 2. Divide each term of the polynomial by the monomial.
Step 3. Simplify.
Example 2
Given f(x) = 2x2 + 4x + 10 and g(x) = 2, find 
.
Step 1. Replace f(x) and g(x) with their equivalent expressions.
Step 2. Divide each term of the polynomial by the monomial.
Step 3. Simplify.
Video Lesson
To learn more on how to multiply and divide functions, please select the following link:
Guided Practice
To solidify your understanding of function operations, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Answer Key
Sources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Multiplying and Dividing Functions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=7172/7172.xml (accessed 8/10/2010).
Holt, Rinehart & Winston, "Properties and Attributes of Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch09_04_homeworkhelp.html (accessed 8/18/2010).
Jenkins, "NutshellMath Homework Help: The Distributive Property." http://www.freemathhelp.com/Lessons/Algebra_1_The_Distributive_Property_BB.htm (accessed 07/18/2010).
Kuta Software, www.kutasoftware.com/free.html (accessed 07/19/2010).
Wilcox, Ted. "HotMath: Using the FOIL Method." 2007. http://www.freemathhelp.com/using-foil.html (accessed 07/18/2010).