Modeling
| Sitio: | Clare |
| Curso: | Michigan Algebra I Sept. 2012 |
| Libro: | Modeling |
| Imprimido por: | Guest user |
| Día: | domingo, 1 de febrero de 2026, 11:47 |
Descripción
Example 1
The velocity of an object fired directly upward is given by V = 80 - 32t, where t is in seconds. When will the velocity be between 32 and 64 feet per second?
Step 1. Set up the compound inequality.
![]()
Step 2. Solve for t.
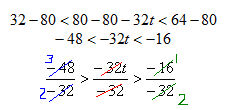
![]()
(Reminder: since the inequality is divided through by a negative,
the inequality signs need to be reversed.)
Step 3. Answer the question.
The velocity will be between 32 and 64 feet per second when the object is between 0.5 and 1.5 seconds after launch.
Example 2
Suppose you have a gift card for $100 to an electronics store and want to spend it on CDs and DVDs. You want a special-edition DVD that costs $24.99, and the CDs you want are all on sale for $11.99 each. Assuming that you use only the gift card and you are going to buy the DVD, what is the maximum number of CDs you can buy?
Step 1. Define the variables.
Let c represent the number of CDs you can buy.
Step 2. Write an inequality to represent the situation and simplify.
Cost of DVD + Cost of each CD•(Number of CDs) ? Amount of Gift Card
24.99 + 11.99c ? 100.00
11.99c ? 75.01
c ? 6.26
Step 3. Answer the question.
6 is the maximum number of CDs that can be purchased using the gift card.
Example 3
The parking fee at a public garage is $5 for the first hour and $3 for each additional hour (or fraction of the hour). How long can you park if you have $14 to spend on parking? Let h represent the number of additional hours after the first hour.
Step 1. Write an inequality to represent the situation.
Price of parking for first hour + $3 times each additional hour (h) ? $14
![]()
Step 2. Solve the inequality.
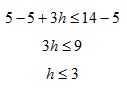
Step 3. Answer the question.
You can park up to 3 additional hours, for a total of 4 hours.
Sources
Chaturvedi, Abhijit. "Solving Linear Inequalities." Connexions. February 5, 2009. http://cnx.org/content/m19599/1.1/
Stapel, Elizabeth. "Solving Linear Inequalities: Advanced Examples." Purplemath. Available from http://www.purplemath.com/modules/
ineqlin3.htm. Accessed 15 August 2010