Inverses
| Site: | Clare |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Inverses |
| Printed by: | Guest user |
| Date: | Tuesday, December 16, 2025, 4:59 AM |
Description
Finding an Inverse
An inverse function is a function that undoes another function, much like addition undoes subtraction. Inverse functions use inverse operations to turn inputs into outputs and vice versa.
The function, f -1 (x), is defined as the inverse function of f(x) if it consistently reverses the process of f(x). That is, if f(x) turns a into b, then f -1(x) must turn b into a. f -1 (x) is not an exponent and is read "the inverse of function f." It is meant to be an inverse function, not a reciprocal.
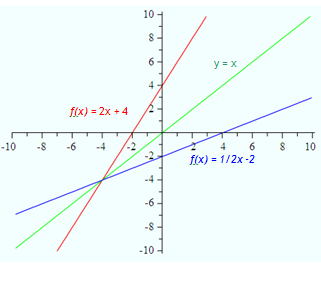
There are a couple of ways to think about the inverse of a function. Inverses can be approached by looking at graphs or performing algebraic operations. In either case, it comes down to the basic notion that the inverse of a function reverses the x and y coordinates. In other words, for every ordered pair (x, y) in a function there will be an ordered pair (y, x) in the inverse function.
The graph of an inverse of a function is reflected over the line y = x. Reflecting over the line y = x produces the goal of reversing the x and y coordinates.
In the graph below, the original function ![]() is reflected over the line y =x and gives us the inverse function
is reflected over the line y =x and gives us the inverse function ![]() .
.
Examples
Example 1 If a function answers the question: "I have this many spoons, how much do they weigh?" The inverse answers the question: "My spoons weigh this much, how many do I have?"
Example 2 If a function answers the question: "How many hours of music fit on 12 CDs?" The inverse answers the question: "How many CDs do you need for 3 hours of music?"
Example 3 Alice makes $100/day. Use the functionm(t)=100t to answer the question "After 3 days, how much money has she made?"
The inverse question, "If Alice has made $300, how many days has she worked?" gives the same relationship, but reverses the dependent and independent variables. Given any amount of money, divide it by 100 to find how many days she has worked. Use the function of t(m)= m/100 to find the inverse of the function.
Recognizing Inverses
How do you recognize an inverse function?
Let's look at the two functions below:
m(t)=100t and t(m)=m/100
Mathematically, these are inverse functions because they reverse the inputs and outputs.
m(t)=100t ? for 3 hours of work, $300 is made ? (3, 300)
t(m)=m/100 ? when $300 is earned, 3 hours of work was done ? (300, 3)
A common example of inverse functions is the Celsius-to-Fahrenheit conversion:
![]()
where C is the Celsius temperature and F is the Fahrenheit temperature. Input 100°C into the first equation and the output is 212°F. Input 212°F into the second equation the output is 100°C. Therefore they are inverses.
Verifying
Using this "reversal" process, we can test any two functions to see if they are inverses.
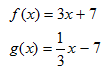
Although they look like inverses, test them to find out if the "reversed" ordered pair is created.
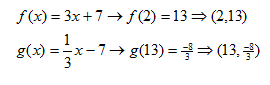
Since the second ordered pair is not the inverse of the first, then g(x) is not the inverse of f(x).
Finding the Inverse
To find an inverse symbolically:
1. Substitute y for f(x).
2. Interchange the x and y variables - this is the foundation behind inverses.
3. Solve the new equation for y.
4. Substitute f-1(x) for y.
Example 1 Find the inverse of the function f(x) = 5x -2.
Step 1. Write the original function using y notation.
Step 2. Interchange x and y.
Step 3. Solve the new equation for y.
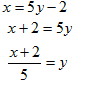
Step 4. Simplify if possible and change to inverse function notation.
![]()
Example 2
Find the inverse of ![]()
Step 1. Write the original function using y notation.
Step 2. Interchange x and y.

Step 3. Solve the new equation for y.
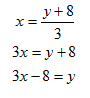
Step 4. Simplify if possible and change to inverse function notation.
Video Lesson
To learn how to find the inverse of a function, select the following link:
Graphing Inverses
The inverse of a function differs from the function in that all the x-coordinates and y-coordinates have been switched. That is, if (4,6) is a point on the graph of the function, then (6,4) is a point on the graph of the inverse function. The graph of a function and its inverse are mirror images of each other. They are reflected about the line y = x.
Video
To learn how to graph the inverse, select the following link:
Guided Practice
To solidify your understanding of inverse functions, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Felder, Kenny. "Function Concepts -- Inverse Functions." Connexions. March 23, 2010. http://cnx.org/content/m18198/1.3/
Holt, Rinehard, & Winston. "Inverse Funcitons."http://my.hrw.com/
math06_07/nsmedia/homework_help/alg2/alg2_ch07_02_homeworkhelp.html (accessed August 14, 2010)
Jones, James. "Inverse Functions." http://people.richland.edu/james/lecture/
m116/functions/inverses.html (accessed August 14, 2010).
Mainland High School, Algebra Lab. "Inverse Functions." http://www.algebralab.org/lesson/lesson.aspx?file=Algebra_FunctionsRelationsInverses.xml (accessed 08/22/2010).