Print bookPrint book

Slope-Intercept Form

Site: Clare
Course: Michigan Algebra I Sept. 2012
Book: Slope-Intercept Form
Printed by: Guest user
Date: Saturday, April 27, 2024, 9:40 PM

Description

Table of contents

Introduction

A linear equation in slope-intercept form is written as y = mx + b. For any equation of the form y = mx + b, the slope of the line is m, or the coefficient of x. The y-intercept is (0, b). The equation y = mx + b is called the slope-intercept form of a straight line


Writing the Equation

To write an equation when given the slope and y-intercept, replace m with the given slope and b with the given y-intercept in the equation y = mx + b.

Example Write an equation in Slope-Intercept form given y-intercept of (0,5) and slope = 2.

(0,5) is the y-intercept, therefore b = 5

Slope = 2, therefore m = 2

y = mx + b

y = 2x + 5

Equation from Points

To find the equation of a line when given two points on the line, use the slope formula to determine the slope, m. Substitute one point and the slope into the slope-intercept form equation and solve for b. Rewrite the equation with m and b. Here are the steps to follow:

  1. Use the two points to find the slope (rate of change) using the slope formula slope_I_twoPoints .
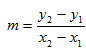  2. Substitute the value of m and the values of (x,y) for one point into the slope-intercept form, y = mx + b, and solve for b.
  3. Substitute the values of m and b into the slope-intercept form equation.
  4. Substitute the other point into the equation to check the values of m and b.


Example

Write the equation of the line containing the points (3, 2) and (-2, 4) in slope-intercept form.

Step 1. Findthe slope of the line, m using the slope formula.

slope_I-ex1


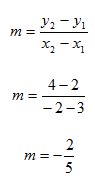
Step 2. Substitute the values for one point (3, 2) and the value for m of slope_I_ex1-2 into the slope-intercept form and solve for b.

slope_I_ex2.1


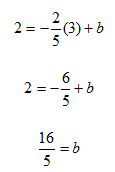
Step 3. Substitute m and b into the slope-intercept form.

slope_I-ex1-3

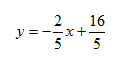
Step 4. Check the solution by substituting values of the second point into the equation.

slope_I-ex1-4

Video Lesson

To learn how to write equations in slope-intercept form, select the following link:

Writing Linear Equations in Slope-Intercept Form

Using Slope-Intercept Form

When the equation of a line is in slope-intercept form the graph can be drawn using the slope, m, and y-intercept. Remember that slope is a ratio representing the amount the line "rises" over how much it "runs" or rise_run .

Example Graph y = -2x + 3 using the slope and y-intercept.

Step 1. Determine the slope and y-intercept and convert the slope to a fraction.

m = slope_I-graph_1 and b = 3

The slope means the graph will go "down two" and "to the right one" for each new point.

To Graph:

Step 1. Begin with the y-intercept, (0, 3)

Step 2. Using slope, go down two and right one to get the next point, (1, 1).

slope_I_graph_1_001


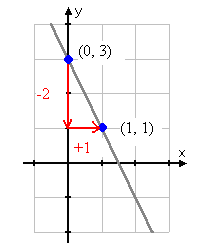
Third Point

Two points are required to make a line, but a third can be found by going down another two, and right another one, to get another point on y = -2x + 3.

third_point

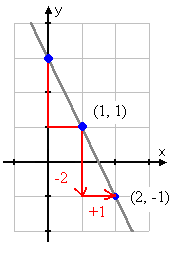
Then the point (2, -1) is also on this line; with three points, we can graph a more accurate line.


Video Lesson

To learn how to graph a function using slope intercept form, select the following link:

Graphing by Using Slope and y-Intercept

Finding Slope & Intercept

The graph of a linear equation is the set of points that correspond to all ordered pairs that satisfy the equation. The graph gives a "picture" of the equation. From the graph the slope and y-intercept can be determined and the equation discovered.

find_slope_intercept

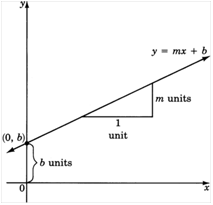
To determine the equation of a line from its graph, find the y-intercept and the slope of the line. Substitute these values in for b and m in the slope-intercept equation and it will represent the line graphed.


Example 1

Find the equation of the line graphed below.

find_slope_intercept_ex1-1

Step 1. Find b

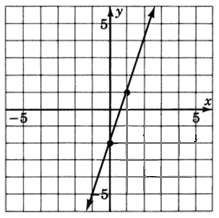
(0,-2) is the y-intercept so b = -2

Step 2. Find slope, m

find_slope_intercept_1-2

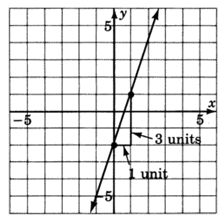
rise = 3 and run = 1 so m = find_slope_intercept_1-3 or 3

Step 3. Write the equation using the slope-intercept form.

y = mx + b
y = 3x - 2


Example 2

Find the equation of the line graphed below.

Find_slope_intercept_ex2-1

Step 1. Find b

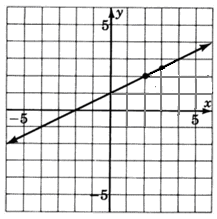
(0,1) is the y-intercept so b = 1

Step 2. Find slope, m

Find_slope_intercept_ex2-2

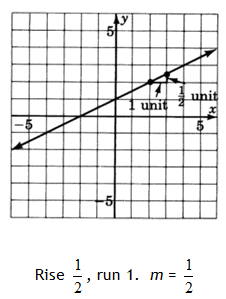
Step 3. Write the equation using the slope-intercept form.

Find_slope_intercept_ex2-3

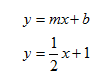
Interactive Activity

To practice graphing lines using slope-intercept form, select the following link:

Graphing the Line y = mx + b

Guided Practice

To solidify your understanding of graphing using slope-intercept form, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice

Graphing Horizontal Lines

What happens to the slope-intercept equation when m = 0? Remember that slope is the ratio of rise over run. For a slope to be zero, then the rise must be zero. In other words the line does not rise, which means it must be horizontal. Plugging m = 0 into the slope-intercept equation produces the following equation:

Graphing_hor_1

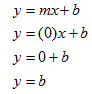
Consider the equation y = 4. There is no x-term, thus m = 0 and b = 4. So the graph will be a line that crosses the y-axis at 4 and does not rise.

Graphing_hor_2

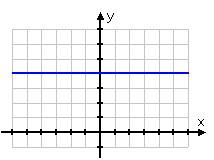
Using the points (-3, 4) and (5, 4), to calculate the slope of this line confirms that the slope of this line is zero.

Graphing_hor_3

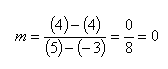
All horizontal lines have a slope of zero. The line above contains the points (-1, 4), (0, 4), (1, 4), (2, 4), etc. Notice that the y-value is always 4. Therefore the equation of a horizontal line will have the form y = b. For example, y = -3 will graph as a horizontal line crossing the y-axis at -3.


Graphing Vertical Lines

If horizontal lines occur when there is no rise, when do vertical lines occur? Vertical lines rise, but do not run. The slope formula for a vertical line is rise_0 , which is undefined. So the equation of a vertical line does not fit within the parameters of the slope-intercept equation, because the slope is undefined. Consider the vertical line below:

Graphing_ver_1

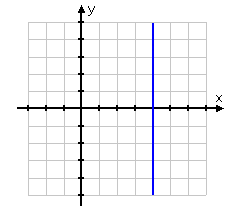
This line contains the points (4, -1), (4, 0), (4, 1), (4, 2), etc. Notice that the x-value is always 4. The equation of this line is x = 4. The equation of a vertical line will always have the form x = "a constant". For example x = -2, will have a graph of a vertical line crossing the x-axis at -2.


Interactive Activity

Explore the graphs of linear equations in slope-intercept form.

Practice

Graphing Lines in Slope-Intercept Form Worksheet

*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.

Practice Answers

Graphing Lines in Slope-Intercept Form Answer Key

*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.




Sources

Ellis, W., & Burzynski, D.2009. Graphing Linear Equations and Inequalities: The Slope-Intercept Form of a Line. Connexions, June 1, 2009. http://cnx.org/content/m22014/1.4/.

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

Gloag, Anne and Andrew. "Writing Linear Equations." December 9,2009. http://www.ck12.org/flexr/flexbook/738/

Holt, Rinehart, & Winston. "Linear Functions. "http://my.hrw.com/math06_07/
nsmedia/homework_help/alg1/alg1_ch05_06_homeworkhelp.html (accessed August 11, 2010)

Stapel, Elizabeth. "Using Slope and y-Intercept to Graph Lines." Purplemath. Available from http://www.purplemath.com/modules/slopgrph.htm. Accessed 11 August 2010

Stapel, Elizabeth. "Slope of a Straight Line." Purplemath. Available from http://www.purplemath.com/modules/slope.htm. Accessed 11 August 2010