Characteristics

The graph of any quadratic function has a "U" shape and is called a parabola. Parabolas always have a line of symmetry that passes through the parabola's vertex. In all parabolas that are considered to be functions, this line of symmetry will be vertical and have an equation in the form x = h, where h is the x-coordinate of the vertex.

The specific values of a, b, and c control where the curve is relative to the origin (left, right, up, or down), and how rapidly it spreads out. Also, if the value of a is negative then the parabola will be reflected across the x-axis before it is translated left, right, up or down.

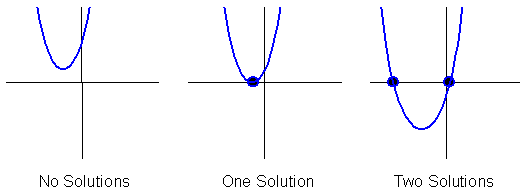
All quadratic functions have one y-intercept and two, one or no x-intercepts. The x-intercepts of the graph are the same as the solutions of the corresponding quadratic equation. Solutions to quadratic equations can also be called roots. Quadratic equations can have two, one, or no real roots. The figures below demonstrate the different solution sets of a quadratic equation.